RSA暗号

公開鍵暗号とは

公開鍵暗号 とは、暗号化と復号に異なる鍵を用いる暗号方式です。暗号化に用いる鍵を公開鍵 、復号に用いる鍵を秘密鍵と呼びます。
公開鍵は、その名の通り、誰でも知ることができる鍵です。一方、秘密鍵は、こちらもその名の通り、秘密にしておく必要がある鍵です。 公開鍵暗号を用いた通信の手順は次のようになります。

1. 通信によって文章を受け取る側が、用意した秘密鍵を元にして公開鍵を作成し、公開する。
2. 通信によって文章を送る側が、公開されている公開鍵を用いて文章を暗号化し、送信する。
3. 受信者は、自分が持っている秘密鍵を用いて暗号文を復号し、文章を読む。

もし、秘密鍵を知らない第三者が暗号化されたデータを傍受したとしても、公開鍵から秘密鍵を求めることは困難です(逆に秘密鍵から公開鍵を作ることは容易で、上の手順で言うと 1. において受信者が実際にそれを行っています)。 したがって、公開鍵暗号を用いることで、秘密鍵を知っている受信者だけがデータを復号できるようにすることができます。

ヒント

なぜ公開鍵暗号では公開鍵と秘密鍵の両方を用いるのでしょうか？ 実は、公開鍵暗号が提案されるまでは、受信者と送信者があらかじめ共通の鍵をやりとりしておき、暗号化と復号で同じ鍵を用いるという共通鍵暗号が使われていました。しかし、共通鍵暗号では、鍵を送る際に第三者に傍受されると、その鍵を用いて暗号化されたデータを復号されてしまうという問題がありました。
そこで、公開鍵暗号では、鍵を送る際に第三者に傍受されても、その鍵を用いて暗号化されたデータを復号されることがないようにするために、公開鍵と秘密鍵の両方を用いるようになりました。

RSA暗号のしくみ

ここではRSA暗号のしくみを説明します。

ヒント

きちんと理解するためには高校数学程度の知識が必要になります。興味がなければ、ここは読み飛ばして次の「文字コード」に進んでも大丈夫です。

RSA暗号では公開鍵と秘密鍵が複数の自然数で表されます。それらがどんな数であるかを順を追って説明します。
まず、相異なる大きな素数 $p$ と $q$ を考えます。これらの積を $n = pq$ とします。また、

$$\phi(n) = (p-1)(q-1)$$

( $\phi (n)$ はオイラー関数と呼ばれます)と互いに素な自然数 $e$ を1つとります。このとき、 $e$ と $\phi(n)$ は互いに素なので、

$$de - k\phi(n) = 1$$

となる自然数 $k$ と $d$ が存在します。
さて、RSA暗号では、 $e$ と $n$ を公開鍵、 $p$ と $q$ と $d$ を秘密鍵とします。このとき、平文(暗号化したい文) $M$ に対して、暗号文 $C$ は

$$C \equiv M^e \mod n$$

で計算されます。送信者は公開鍵 $e$ と $n$ を使って暗号化するということです。また、暗号文 $C$ に対して、元の平文 $M$ は

$$M \equiv C^d \mod n$$

で計算されます。受信者が秘密鍵 $d$ を使って復号するということです。
$M \equiv C^d \mod n$ が成り立つのはなぜでしょうか。$C^d$を計算してみると、

$$C^d = M^{de} = M^{k\phi(n) + 1} = M^{k(p-1)(q-1) + 1} = (M^{k(q-1)})^{p-1} \cdot M$$

となりますが、 $p$ が十分大きな素数であるとき、フェルマーの小定理(下のヒントを参照)より、

$$(M^{k(q-1)})^{p-1} = 1 \mod p$$

です。したがって

$$C^d \equiv 1 \cdot M \equiv M \mod p$$

となります。よって $C^d - M$ は $p$ の倍数です。同様にして $C^d - M$ は $q$ の倍数でもあります。したがって、 $C^d - M$ は $n = pq$ の倍数です。よって、 $C^d \equiv M \mod n$ であることがわかりました。

ヒント

フェルマーの小定理とは、 $p$ を素数、$a$ を $p$ の倍数でない整数とすると、

$$a^{p-1} \equiv 1 \mod p$$

が成り立つという定理です。$p$ が十分大きな素数であれば、$M < p$ となり、$M^{k(q-1)}$ は $p$ の倍数でないので、この定理を用いることができます。なお、実際にRSA暗号を用いるとき、$M$ は次で説明する文字コードの値になることから、どんな $M$ よりも大きい素数であるような $p$ を選ぶことが可能です。

注記

公開鍵 $n$ を公開してしまうと、$n=pq$ という関係から 秘密鍵の $p$ と $q$ が求められてしまうと感じるかもしれません。これは $n$ を素因数分解することと同じです。しかし、$p$ と $q$ が十分大きいとき、$n=pq$ を素因数分解することは一般には困難です。 少なくとも現在は、たとえコンピュータを用いたとしても、大きい $n$ の素因数分解にかかる時間は非常に長くかかります。 このように、RSA暗号は、素因数分解の困難性を利用した暗号方式になっています。

文字コード

文字コードとは、文字をコンピュータで扱うために、文字に対応する数値を定めたものです。文字コードには様々なものがありますが、ここでは、ASCIIコードとUnicodeを紹介します。

ASCIIコード

ASCIIコードは、アルファベット、数字、記号などの文字をコンピュータで扱うために、それぞれの文字に対応する7ビットの数値(0～127の128通り)を定めたものです。
例えば大文字の 'A' は、ASCIIコードでは 65 と定められています。
また、小文字の 'a' は、ASCIIコードでは 97 と定められています。 ASCIIコードでは、アルファベットの大文字と小文字は、それぞれ、65 から 90 まで('A'～'Z')の数値と、97 から 122 まで('a'～'z')の数値に対応しています。
また、'0'～'9'の数字は、それぞれ 48~57までの数値に対応しています。
また、記号の中で、例えば '!'は 33、'?'は 63、'+'は 43、'-'は 45、'/'は 47、'='は 61 にそれぞれ対応しています。
その他にも、改行を表す文字や、スペース、タブなどの、制御文字と呼ばれる特殊な文字にも、対応する数値が定められています。

Unicode

ASCIIコードが扱えるのは、アルファベット、数字、およびいくつかの記号などに限られます。先ほども述べたように、ASCIIコードで使える数値は128通りしかありません。しかし、今あなたがコンピュータの画面上で読んでいる文章は、ひらがなやカタカナ、そして漢字が使われています。漢字だけでも128通りは優に超えますし、また世界には他にも多くの文字があります。
これらの文字のように、世界中で使われている様々な文字をもコンピュータ上で扱うために、ASCIIコード以外にも色んな文字コードが考案されています。 その代表的な規格として Unicode があります。Unicode の文字に対応する数値を定める方式として、UTF-8、UTF-16、UTF-32などがありますが、ここでは UTF-8 について説明します。

UTF-8

UTF-8では、8ビットの値(0～255)を1つの符号単位として、1～4の符号単位を用いて1つの文字を表します。
例えばASCIIコードにもあった'A'は、1つの符号単位を用いて 65 と表されます(ASCIIコードと同様)。
また、ひらがなの'あ'は、3つの符号単位を用いて 227, 129, 130 と表されます。
さらに絵文字を表すこともでき、例えば'😊'は、4つの符号単位を用いて 240, 159, 152, 138 と表されます。

RSA暗号の使い方

RSA暗号の使い方を説明します。先ほども述べたように、RSA暗号では公開鍵 $e$ と $n$ 、および秘密鍵 $p$ と $q$ と $d$ を用います。ここでは、

$$e=13, n=2987, p=29, q=103, d=2197$$

とします(「RSA暗号のしくみ」を読んだ人は、これらが $n=pq$ などの条件を満たしていることを確認してみるとよいでしょう)。では、これらの鍵を用いて "こんにちは" という文字列を暗号化し、できた暗号を復号してみましょう。

エンコード

まず、UTF-8を用いて "こんにちは" を数字の列に変換します。このことをエンコードといいます。'こ'は、 227, 129, 147 に変換されます。'ん'は、 227, 130, 147 に変換されます。以下同様に変換していくと、"こんにちは"は全体として

$$227, 129, 147, 227, 130, 147, 227, 129, 171, 227, 129, 161, 227, 129, 175$$

に変換されます。

暗号化

続いて暗号化を行います。暗号化では、エンコードによって得られた数をそれぞれ $e$ 乗して、 $n$ で割った余りを求めます。例えば、最初の 227 は、227 の 13 乗を 2987 で割った余りを計算することになります。これは手計算で行うのは大変ですが、コンピュータや電卓を使って計算すると 1821 になることがわかります。同様にして、2つ目以降の数についても 13 乗して 2987 で割った余りを計算すると、全体として

$$1821, 328, 2740, 1821, 2612, 2740, 1821, 328, 2910, 1821, 328, 2833, 1821, 328, 1451$$

となります。つまり、これが "こんにちは" を暗号化したものになります。

復号

次に、この暗号を復号します。復号では、数を $d$ 乗して $n$ で割った余りを求めます。例えば、最初の 1821 は、1821 の 2197 乗を 2987 で割った余りを計算することになります。これもコンピュータや電卓を使って計算すると、 227 になることがわかります。同様にして、2つ目以降の数についても 2197 乗して 2987 で割った余りを計算すると、全体として

$$227, 129, 147, 227, 130, 147, 227, 129, 171, 227, 129, 161, 227, 129, 175$$

となります。つまり、これが "こんにちは" を復号したものになります。

デコード

最後に、これらの数を文字に変換します。つまりエンコードの逆の操作を行います(これをデコードといいます)。復号した結果の最初の3つの数は 227, 129, 147 ですが、これは 'こ' に対応する数です。同様にして、2つ目以降の数についてもデコードすると、全体として"こんにちは"となります。よって、RSA暗号を用いて文字列を暗号化し、復号することができました。

実際にやってみよう

それでは、実際にRSA暗号を用いて文字列を暗号化し、復号してみましょう。 RSA暗号にアクセスしてください。次のような画面が表示されます。

RSA暗号を体験できるサイトを開く

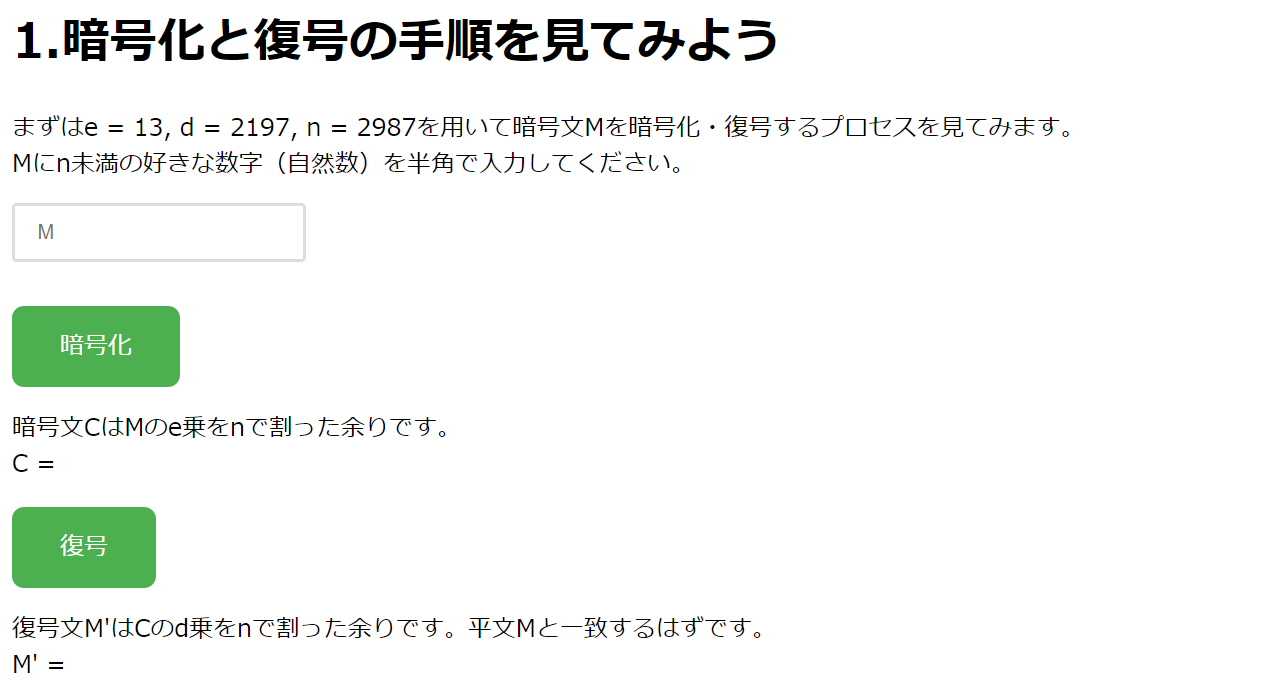まずは指示に従って、$M$ に $n$ 未満の好きな数を入れましょう。その後、「暗号化」のボタンをクリックすると、$C$ に $M$ の $e$ 乗を $n$ で割った余りが表示されます。続いて、「復号」のボタンをクリックすると、$M'$ に $C$ の $d$ 乗を $n$ で割った余りが表示されます。
すると、$M$ と $M'$ が一致することがわかります。今は $M$ はただの数なのであまり実感は沸かないかもしれませんが、$M$を暗号化したもの($C$)を復号するとちゃんと $M$ に戻っていることがわかります。
次に2番に進みます。

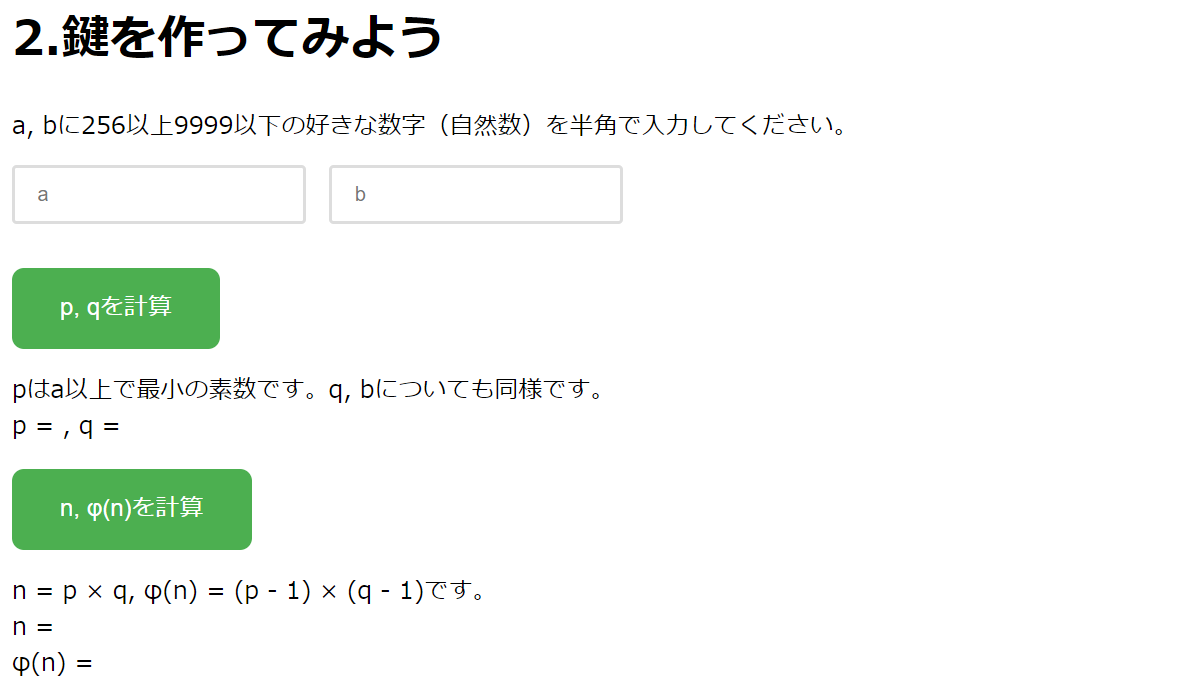先ほどはRSA暗号の鍵が与えられていましたが、ここでは鍵を作ってみましょう。$a$ と $b$ に、256～9999の好きな数を入力し、「$p, q$ を計算」のボタンをクリックしてください。すると、$p$ と $q$ が表示されます。 このとき表示される $p$ は $a$ 以上の素数のうち最小のものです。同様に、$q$ は $b$ 以上の素数のうち最小のものです。ただし、$p$ と $q$ は同じ数になってしまった場合は、自動的に再計算されて異なる数になります。なお、$p$ と $q$ が文字コードの値よりも大きくなるようにするために、$a$ と $b$ は256以上の数に限定しています。 続いて、「$n, \phi(n)$ を計算」 のボタンをクリックすると、先ほどの $p$ と $q$ から $n$ と $\phi(n)$ が計算されます。

次に、「$e$ を計算」のボタンをクリックすると、$\phi(n)$ と互いに素な $e$ が計算されます。ここではそのような $e$ のうち最小のものが表示されます。 最後に、「$d$ を計算」のボタンをクリックすると、$e$ を $\phi(n)$ で割った余りとして $d$ が計算されます。
これで、RSA暗号の鍵がすべて揃いました！ それでは3番に進みましょう。

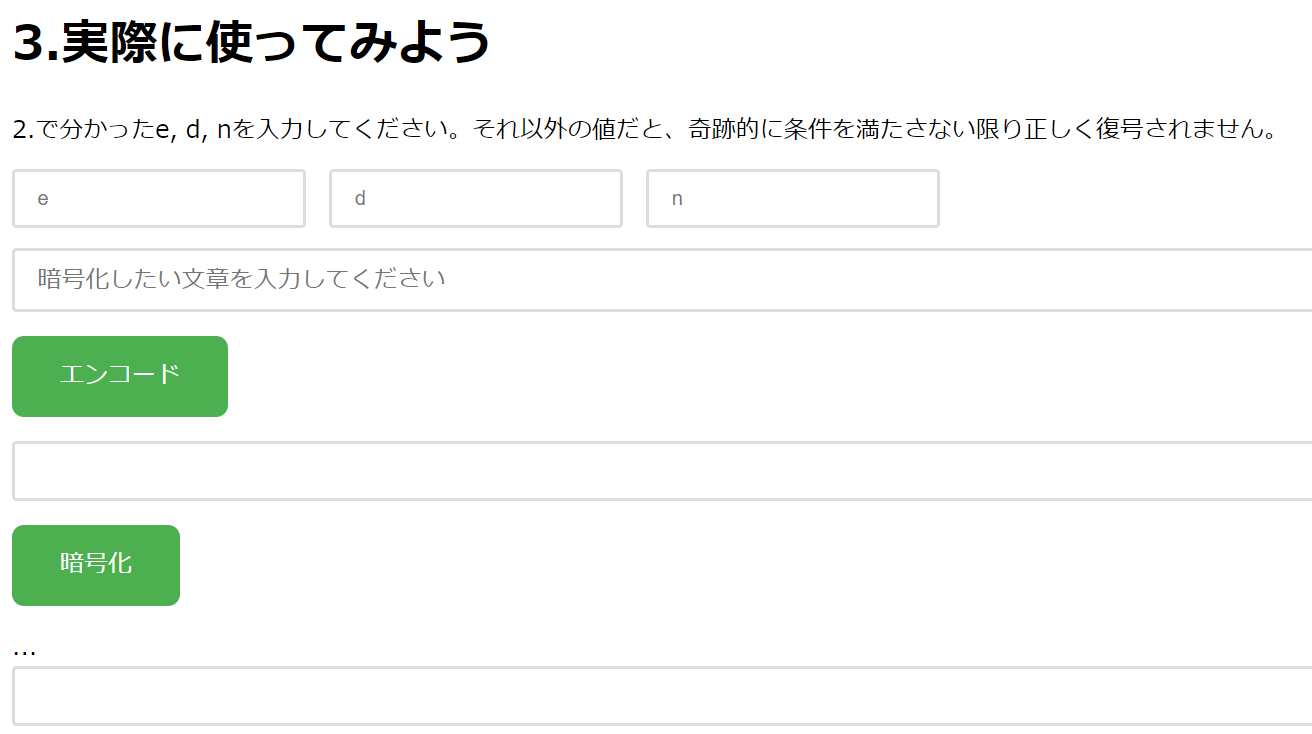まず、先ほど決めた鍵である $e$、$d$、$n$ を入力し、また暗号化したい文字列を入力します。 次に、「エンコード」のボタンをクリックすると、文字列がエンコードされて数の列に変換されます。 そして、「暗号化」のボタンをクリックすると、エンコードされた数の列が暗号化されます。

次に、「復号」のボタンをクリックすると、暗号化された数の列が復号されます。 最後に、「デコード」のボタンをクリックすると、復号された数の列が文字列に変換されます。 元の文字列に戻りましたか？ もし戻っていなければ、鍵の入力が正しいか確認し、やり直してみましょう。

ここまで、RSA暗号について学び、実際に使ってみました。これでみなさんも、RSA暗号を用いて文字列を暗号化し、復号することができるようになりました。おめでとうございます！